Capacitated Facility Location Problem

Posted on | In | 浏览 次
Words count in article: 2.4k | Reading time ≈ 10

项目地址

介绍

Suppose there are n facilities and m customers. We wish to choose:

  • which of the n facilities to open
  • the assignment of customers to facilities

The objective is to minimize the sum of the opening cost and the assignment cost.

The total demand assigned to a facility must not exceed its capacity.

分析

该问题阐述的比较明确，目前有n个设备，每个设备开启需要一个固定的费用，然后又有m个顾客，每个顾客有一定的需求，但是每个设备能够提供的资源是有限的，并且每个顾客使用相应的设备的时候还需要提供一笔附加的费用，此处还有一个前提条件是一个顾客所有需求只能被一个设备处理。目前的问题是，如何给顾客分配设备，使得最后总费用最小。

这是一个NP-hard的问题，给出一种分配方式，我们可以比较容易的确定其是否可行，但是如果想要找到一个最理想的分配方案，则是非常的难的，我们只能尽可能的找到一个比较理想的解。最近在用模拟退火(SA)与遗传算法(GA)解决另一个比较经典的问题-TSP问题，所以本次也就优先想到使用这两种算法来搜索得到一个比较理想的解，但是这些最终解都是当前解里面最优的，为相应算法中的最优解，并非全局最优 。

解决

关于模拟退火算法以及遗传算法的具体流程就不再详细，都是比较经典的算法，接下来主要讲讲与问题相关联的核心部分思路与实现

模拟退火 (SA)

模拟退火算法以一定的概率来接受一个比当前解要差的解，因此有可能会跳出这个局部的最优解，达到全局的最优解。

在本次算法设计中，比较关键的点在于搜索中领域操作的设计上，领域操作影响着最终结果的好坏，通过邻域动作。产生初始解的邻居解，然后根据某种策略选择邻居解。一直重复以上过程，直到达到终止条件。对于本次场景而言，对于产生的解，只要是新解所需要的费用小于目前的费用，则直接选择该接。而对于一些比当前的解要差的解，以一定的概率接受，采纳的概率为:

本次模拟退火算法设计中，所设计的领域操作位在用户序列中随机选择两个位置，对于在此之间的用户为其重新随机选择一次所选择的设备，如果随机到的设备所能提供的容量不满足，则再次随机选择设备，直到选择到合适的为止，该领域操作尽可能的涉及到了各种可能的分配方案，尽可能的扰动当前结果以及概率接受差解，使其可能跳出局部最优解，已得到比较理想的解。

模拟退火算法主要核心代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
// 模拟退火
while(T > 0.01) {
    /* 扰动获得寻找较优解，并且可能接收差解 */
    int i = 0;
    while(i++ < SEARCHTIMES) {
        int first = rand() % (p->numOfCus);
        int second = rand() % (p->numOfCus - first) + first;
        vector<int> newCusToFac = cusToFac;
        vector<int> newFreeCapacity = freeCapacity;

        // 回收容量
        for(int j = first; j <= second; ++j)
            newFreeCapacity[newCusToFac[j]] += p->cusDemand[j];

        // 随机分配一个新的工厂
        for(int j = first; j <= second; ++j) {
            int newFac = rand() % (p->numOfFac);
            while (p->cusDemand[j] > newFreeCapacity[newFac])
                newFac = rand() % (p->numOfFac);
            newCusToFac[j] = newFac;
            newFreeCapacity[newFac] -= p->cusDemand[j];
        }

        int cost = calCost(p, newCusToFac, newFreeCapacity);
        double probability = (rand() % 100) * 1.0 / 100;

        // 处理当前解，一定概率接受
        if (cost <= totalCost || probability < exp(-abs(cost-totalCost) / T)) {
            cusToFac = newCusToFac;
            freeCapacity = newFreeCapacity;
            totalCost = cost;
        }
    }
    // 降温
    T *= alpha;
}

关于SEARCHTIMES，局部搜索的次数设置也比较关键，搜索次数也影响着结果的好坏，如果次数太少则可能造成遗漏比较多，而次数设置的比较大的话，对于数据量比较小的情况将造成算力浪费。因此考虑到可能出现的随机情况$C^2_n$，因此对于不同问题，动态设置局部搜索的次数为SEARCHTIMES = n * (n-1) / 2，但是其实还是很耗时，但是效果还可以。

遗传算法 (GA)

关于遗传算法解决，其实个人认为普通的遗传算法效率并不高，并且如果没有针对问题有一定的设计的话，很难达到比较好的状态。

首先需要大概的了解遗传算法的主要流程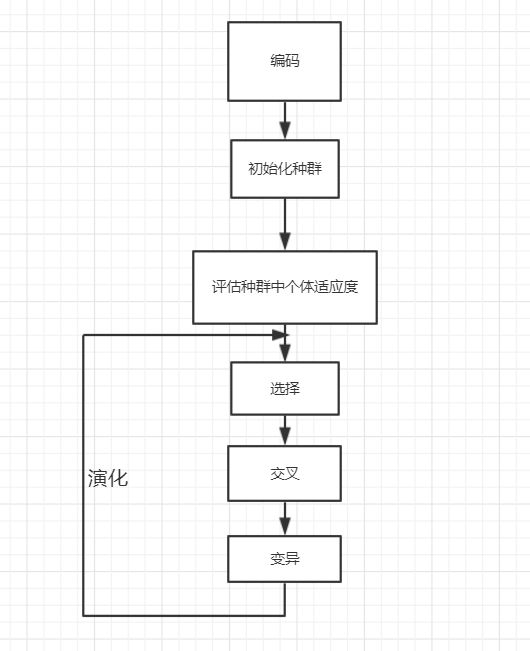
GA

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
// 初始化种群
initPopulation(p);

// 模拟遗传
int curGen = 0;
while(curGen < MAXGEN) {
    // 选择
    select(p);
    // 交叉
    crosscover(p);
    // 变异
    mutate(p);
    ++curGen; 
}

关于适应度评估，其适应度等于该方案费用cost的倒数，即1 / cost

关于选择，使用比较通用的轮盘赌，同时选择其他的选择策略的效果也是不错的

关于种群初始化，其实默认是比较容易的，即随机生成种群即可，但是实验起来发现随机生成初始种群，其收敛效果很差并且效率很低。因此在初始化种群的时候加入部分贪心生成的个体，加快种群成熟速度，也保证了种群中个体的多样性。关于贪心生成个体的思路也比较简单，打乱顾客挑选设备的顺序，每次未顾客挑选当前所需要费用最小的设备。但是关于贪心生成的较优个体的占额也需要注意，如果占的比列比较大，可能会导致过早收敛，出现早熟现象。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
// 初始化种群
void initPopulation(problem* p) {
    // 为提高效率，初始时候通过贪心加入一部分较优个体

    // 随机生成解
    for(int i = 0; i < POSIZE / 2; ++i) {
        individual* ind = new individual(p);
        for(int j = 0; j < p->numOfCus; ++j) {
            int fac = rand() % (p->numOfFac);
            while (p->cusDemand[j] > ind->freeCapacity[fac])
                fac = rand() % (p->numOfFac);
            ind->freeCapacity[fac] -= p->cusDemand[j];
            ind->cusToFac[j] = fac;
        } 
        evalute(p, ind);
        population.push_back(ind);      
    }

    // 贪心生成解
    vector<int> temp;
    for(int i = 0; i < p->numOfCus; ++i) temp.push_back(i);
    for(int i = 0; i < POSIZE / 2; ++i) {
        individual *ind = new individual(p);
        random_shuffle(temp.begin(), temp.end());
        for(int j = 0; j < p->numOfCus; ++j) {
            int mixCost = INT_MAX;
            for(int k = 0; k < p->numOfFac; ++k) {
                if (p->cusDemand[temp[j]] <= ind->freeCapacity[k] && mixCost >= p->useCost[temp[j]][k]) {
                    mixCost = p->useCost[temp[j]][k];
                    ind->freeCapacity[k] -= p->cusDemand[temp[j]];
                    ind->cusToFac[temp[j]] = k;
                }
            }
        }
        evalute(p, ind);
        population.push_back(ind);
    }
    random_shuffle(population.begin(), population.end());
}

关于交叉操作，第n条染色体与第n+1条染色体有一定的概率进行交叉(n = 0, 2, 4, ..., 2n)。这部分使用两点交叉

两点交叉（Two-point Crossover）：在个体编码串中随机设置了两个交叉点，然后再进行部分基因交换

但是交叉后的结果可能是不可行的方案，我们需要判断一下交叉后的解是否可行，然后再进行一定的策略操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
// 交叉
void crosscover(problem* p) {
    // 两点交叉 
    vector<individual*> subPopulation;
    for(int i = 0; i < POSIZE / 2; ++i) {
        if ((rand() % 100) * 1.0 / 100 <= PXOVER) {
            int count = 0;
            while(count++ < 100) {
                individual *a = new individual(population[i*2]);
                individual *b = new individual(population[i*2+1]);
                int geneFirst = rand() % (p->numOfCus);
                int geneSecond = rand() % (p->numOfCus - geneFirst) + geneFirst;
                for(int k = geneFirst; k <= geneSecond; k++) {
                    int temp = a->cusToFac[k];
                    a->cusToFac[k] = b->cusToFac[k];
                    b->cusToFac[k] = temp;
                }

                if (validCover(p, a) && validCover(p, b)) {
                    evalute(p, a);
                    evalute(p, b);
                    subPopulation.push_back(a);
                    subPopulation.push_back(b);
                }
            }
        }
    }
    sort(subPopulation.begin(), subPopulation.end(), [&](const individual* a, const individual* b) -> bool{ return a->cost < b->cost;});
    int num = 0;
    for(int i = 0; i < subPopulation.size(); ++i) {
        for(int j = 0; j < POSIZE; ++j) {
            if(population[j]->cost > subPopulation[i]->cost) {
                individual* temp = population[j];
                population[j] = subPopulation[i];
                ++num;
                delete temp;
                break;
            }
        }
    }
    for(int i = num; i < subPopulation.size(); ++i)
        delete subPopulation[i];
}

关于变异，使用最基本的基因变异的原理，种群中每个个体的每个顾客看作一个基因，基因突变则看成为该顾客重新选择一个对应的可用的设备

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// 变异
void mutate(problem* p) {
    for(int i = 0; i < POSIZE; ++i) {
        double pro = (rand() % 100) * 1.0 / 100;
        if(pro <= PMUTATION) {
            for(int j = 0; j < p->numOfCus; ++j) {
                int newFac = rand() % p->numOfFac;
                population[i]->freeCapacity[population[i]->cusToFac[j]] += p->cusDemand[j];
                while (p->cusDemand[j] > population[i]->freeCapacity[newFac])
                    newFac = rand() % (p->numOfFac);
                population[i]->freeCapacity[newFac] -= p->cusDemand[j];
                population[i]->cusToFac[j] = newFac;
            }
        }
    }
}

结果

完整结果

模拟退火算法

Problem Result Time(s)
p1 9075 0.729
p2 8315 0.685
p3 10076 0.684
… … …
p68 26452 51.886
p69 35383 54.413
p70 50826 51.292
p71 39417 51.519

遗传算法

Problem Result Time(s)
p1 10220 10.727
p2 9493 11.888
p3 11653 10.831
… … …
p68 33324 43.275
p69 38309 44.419
p70 59304 38.904
p71 46541 37.729

总结

从结果的运行时间可用比较直观的看出两个算法对于数据量比较大的时候都比较费时，可以控制时间但是会导致解的变差，增大运算此时解可能会更加好，但是时间太长，难以接受