330. Patching Array

题目

Given a sorted positive integer array nums and an integer n, add/patch elements to the array such that any number in range [1, n] inclusive can be formed by the sum of some elements in the array. Return the minimum number of patches required.

Example 1:

Input: nums = [1,3], n = 6
Output: 1 
Explanation:
Combinations of nums are [1], [3], [1,3], which form possible sums of: 1, 3, 4.
Now if we add/patch 2 to nums, the combinations are: [1], [2], [3], [1,3], [2,3], [1,2,3].
Possible sums are 1, 2, 3, 4, 5, 6, which now covers the range [1, 6].
So we only need 1 patch.

Example 2:

Input: nums = [1,5,10], n = 20
Output: 2
Explanation: The two patches can be [2, 4].

Example 3:

Input: nums = [1,2,2], n = 5
Output: 0

解题

• 题意：题目指给出一个有序的正整数的数列nums，以及一个正整数n，最少需要额外添加的多少个数字才能使得[1,n]中每一个数字能够被数列中若干个数字的和表示，求出最少需要添加的数字数。

• 解题思路：假设当前[0, t)中每个数字可以由数列中的数字以及额外添加的数字的和表示，则当其选择到下一个num[i]的时候，分两种情况讨论

  • num[i] <= t
    • 此时可以将维护的区间扩展到[0 , t+num[i] ]

  • num[i] > t

    • 此时不能直接扩展区间，因为中间有一段数字[t, num[i] - 1]是无法表示的。因此此时需要加一个额外的数字，加的数字应该尽可能的大，否则将可能会增加额外需要数字的数目。当前能够加的最大数字是t，因为如果额外添加的数字newNum大于t，则对于区间[t, newNum - 1]这一段的数字则无法表示，因此每次最多加t，区间扩展到[t, t+t]，同时统计添加数字addNum + 1.

    当前维护的t > n的时候，可以直接输出结果

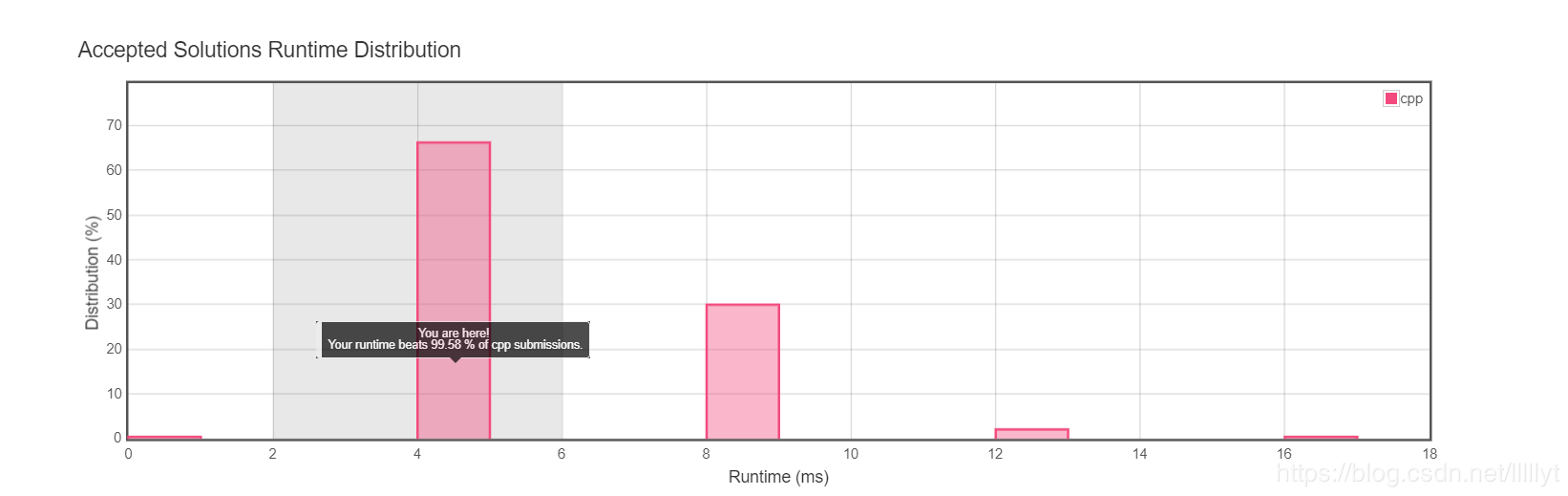
  • 然而，问题并没有解决，出现了超时的问题。对于测试数据感觉还是比较小的，不太可能是由于时间复杂度出错。然后最后的结果是2147483647，接近了int的最大值，考虑到是区间扩展t + t的时候导致溢出，一直导致t < n，出现死循环了，因此将t改为long long类型
    

实现代码

class Solution {
public:
int minPatches(vector<int>& nums, int n) {
    // [0, rightSide)
    long long rightSide = 1;
    int addNums = 0;
    for(auto num : nums) {
        if(rightSide > n)	return addNums;
        while (num > rightSide && rightSide <= n) {
            rightSide += rightSide;
            addNums++;
        }
        rightSide += num;		
    }
    while (rightSide <= n) {
        rightSide += rightSide;
        addNums++;
    }
    return addNums;
}
};

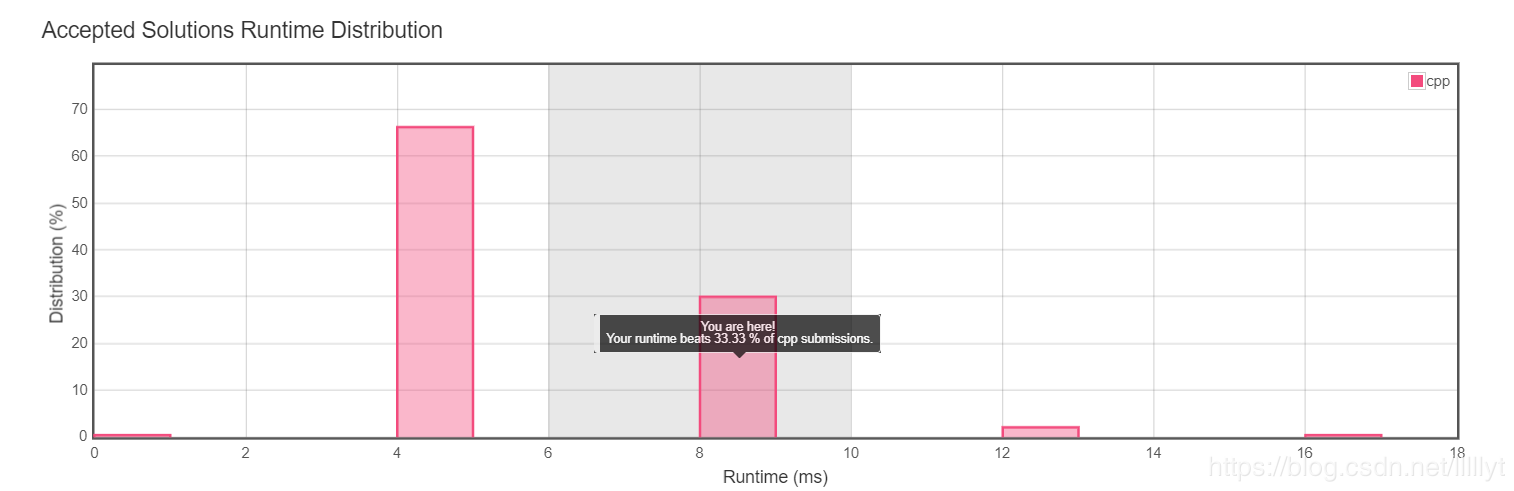
• 感觉写的思路还是比较混乱，然后稍微优化一下代码的结构
• 优化代码
• 谈一个新发现： 本来对于区间扩展部分都是使用+=操作，但是最后运行时间与未优化的没有区别，然后看了下提交的dalao们的代码，发现都是a = a + b这样形式的操作，不使用+=操作的，然后就惊奇的发现运行时间神奇的减少大半了

class Solution {
    public:
        int minPatches(vector<int>& nums, int n) {
        // [0, rightSide)
        long long rightSide = 1;
        int addNums = 0;
        int i = 0;
        int size = nums.size();

        while (rightSide <= n) {
            if(i < size && rightSide >= nums[i]) {
                rightSide = rightSide + nums[i];
                ++i;
            } else {
                rightSide = rightSide + rightSide;
                ++addNums; 
            }
        }
        return addNums;
    }
};