207. Course Schedule |

题目

There are a total of n courses you have to take, labeled from 0 to n-1.

Some courses may have prerequisites, for example to take course 0 you have to first take course 1, which is expressed as a pair: [0,1]

Given the total number of courses and a list of prerequisite pairs, is it possible for you to finish all courses?

Example 1:

Input: 2, [[1,0]] 
Output: true
Explanation: There are a total of 2 courses to take. 
            To take course 1 you should have finished course 0. So it is possible.

Example 2:

Input: 2, [[1,0],[0,1]]
Output: false
Explanation: There are a total of 2 courses to take. 
            To take course 1 you should have finished course 0, and to take course 0 you should also have finished course 1. So it is impossible.

Note:

The input prerequisites is a graph represented by a list of edges, not adjacency matrices. Read more about how a graph is represented.
You may assume that there are no duplicate edges in the input prerequisites.

题目分析

题意比较容易理解，就是需要选修某一门课程的时候，需要先修某一门课程，给出一组课程的先修关系，问是否能完成课程。这个问题可以抽象为有向图求是否有环路问题，课程的先修关系是一个有向边，每一门课程就是一个点。
问题抽象成有向图求是否存在环路问题，思考有向图求存在环路的方法。

拓扑排序实现

什么是拓扑排序？

对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若边(u,v)∈E(G)，则u在线性序列中出现在v之前。通常，这样的线性序列称为满足拓扑次序(Topological Order)的序列，简称拓扑序列。简单的说，由某个集合上的一个偏序得到该集合上的一个全序，这个操作称之为拓扑排序。
为什么用拓扑排序？

如果能够用拓扑排序完成对图中所有节点的排序的话，就说明这个图中没有环，而如果不能完成，则说明有环
怎样进行拓扑排序？
1. 建立图的邻接表
2. 然后找出入度数为0的点
3. 删除入度数为0的点，将其指这些点的边也删除，同时将这些点加入到结果队列中
4. 重复2，直到没有点的入度为0
5. 判断是否仍存在未被加入的点，若存在证明有环
当然本题不需要这么完整的步骤，不需要得到排序结果什么的，只需要最后判断下是否有环，然后返回true或者false
时间复杂度：$O(V+E)$

DFS实现

需要对DFS有一定深入的了解，了解树边，前向边等等
需要DFS稍加变化，来解决这个问题。解决的方法如下：

图中的一个节点，根据其vertexState[i]的值，有三种状态：
点的状态
- -1 - 已被访问过，正在访问其后代节点
- 0 - 未被访问过
- 1 - 已被访问过，且其子节点亦全部访问过
按照这样的假设，当按照DFS进行搜索时，碰到一个节点时有三种可能：

1、如果vertexState[V]=0，这是一个新的节点，未被访问过，进行dfs搜索
2、如果vertexState[V]=-1，说明是在访问该节点的后代的过程中访问到该节点本身，则图中有环。
3、如果vertexState[V]=1，该点已经被访问过，且以该点与其后代节点构成的一个子图是一个非强连通图，则遇到这类点不可能有环存在。
时间复杂度：$O(V)$

实现代码

解法1 - 拓扑排序

拓扑排序思路

// 解法 1

class Solution {
public:
    bool canFinish(int numCourses, vector<pair<int, int>>& prerequisites) {
        if(numCourses <= 1)	return true;
            int n = numCourses;
        vector<set<int> > myVec(numCourses);
        for(auto it : prerequisites)
            myVec[it.first].insert(it.second);

        queue<int> q;

        for(int i = 0; i < numCourses; ++i) {
            if(myVec[i].size() == 0)
                q.push(i);
        }

        while(!q.empty()) {
            int size = q.size();
            n -= size;
            for(int i = 0; i < size; ++i) {
                int tmp = q.front();
                q.pop();
                for (int j = 0; j < numCourses; ++j) {
                    if(j == tmp)	continue;
                    if(myVec[j].find(tmp) != myVec[j].end()) {
                        myVec[j].erase(myVec[j].find(tmp));
                        if (myVec[j].size() == 0) 
                            q.push(j);
                    }
                }
            }
        }

        if(n > 0)
            return false;
        else
            return true;
    }
};

拓扑排序优化 — Course Schedule ll中思路

// 解法 1 优化
class Solution {
public:
    bool canFinish(int numCourses, vector<pair<int, int>>& prerequisites) {
        int inDegree[numCourses] = {0}; // 记录课程需要先修课程的数量

        // 对应存储需要修完该课程才能修的课程
        vector<set<int> > myVec(numCourses);
        for(auto it : prerequisites) {
            inDegree[it.first]++;
            myVec[it.second].insert(it.first);
        }

        queue<int> q;

        for(int i = 0; i < numCourses; ++i) {
            if(inDegree[i] == 0) {
                q.push(i);
            }
        }

        while(!q.empty()) {
            int size = q.size();
            numCourses -= size;
            for(int i = 0; i < size; ++i) {
                int tmp = q.front();
                q.pop();
                // 此处的引用很精髓！！！！
                for (auto &j : myVec[tmp]) {
                    inDegree[j]--;
                    if(inDegree[j] == 0) {
                        q.push(j);
                    }
                }
            }
        }

        return numCourses == 0;
    }
};

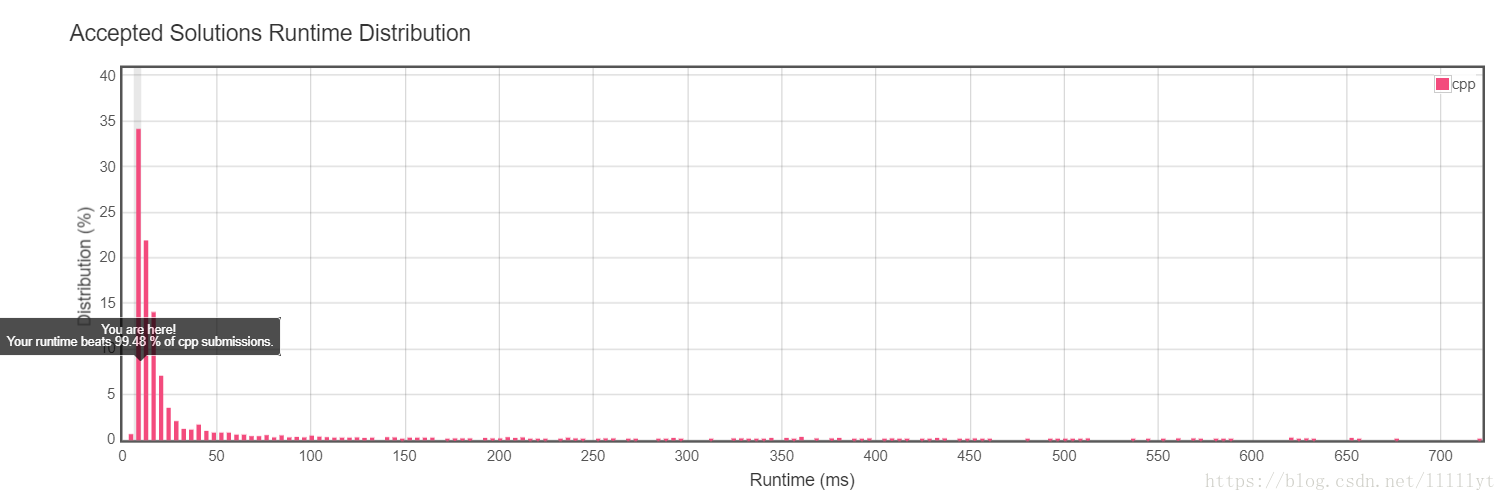
遍历节点度数时候使用引用传递
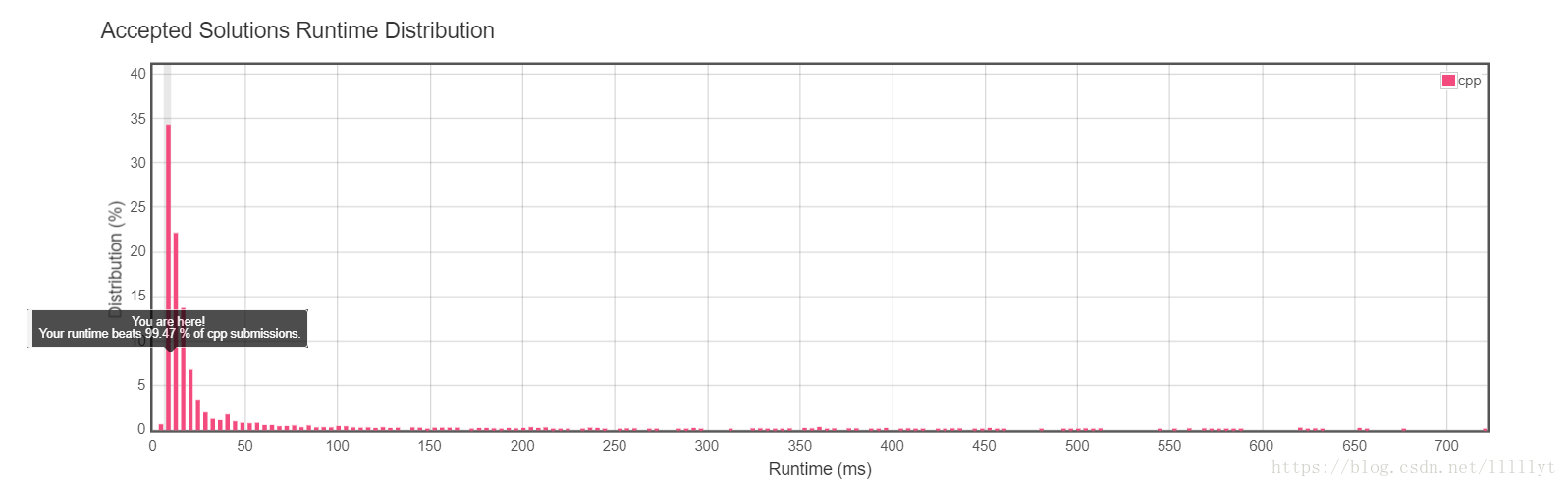
遍历节点度数时候使用值传递
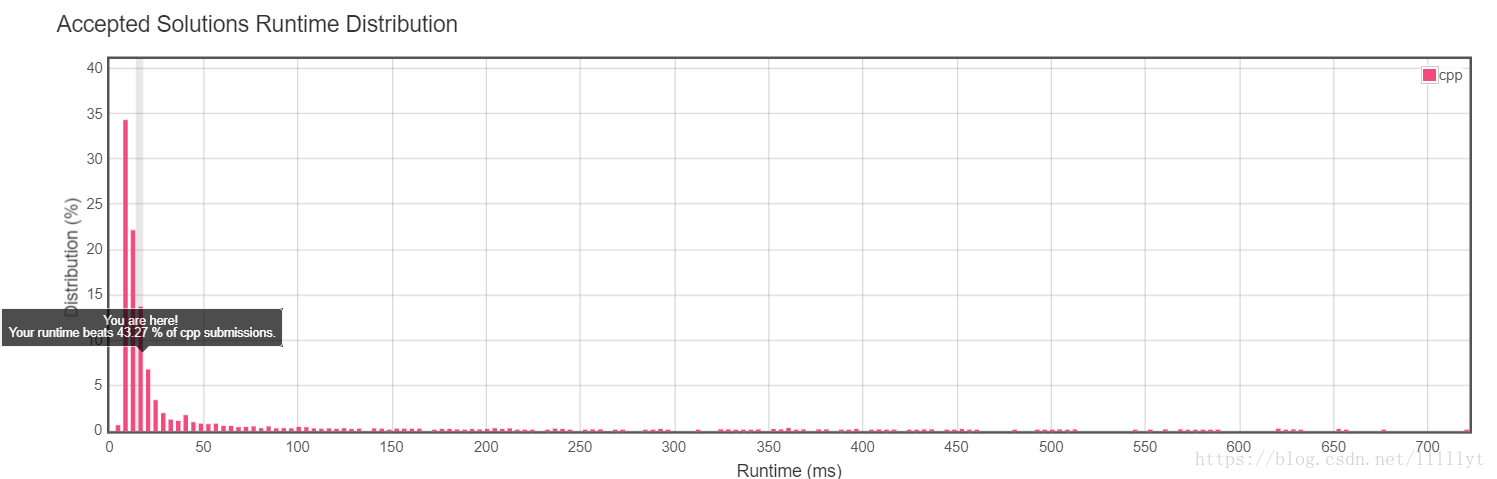
引用传递：在引用传递过程中，被调函数的形式参数虽然也作为局部变量在栈中开辟了内存空间，但是这时存放的是由主调函数放进来的实参变量的地址。值传递：形参是实参的拷贝，改变形参的值并不会影响外部实参的值，形参有自己独立的存储空间，每次都需要在栈中申请内存空间并且拷贝实参。因此，引用传递比值传递需要的操作时间小多了。

解法2 - DFS

优化的DFS实现

// 解法 2
class Solution {
public:
    bool canFinish(int numCourses, vector<pair<int, int>>& prerequisites) {
        vector<set<int> > myVec(numCourses);
        for(auto it : prerequisites)
            myVec[it.second].insert(it.first);
        
        /*
        *	点的状态
        * 	-1 - 已被访问过，正在访问其后代节点
        *	 0 - 未被访问过
        *	 1 - 已被访问过，且其子节点亦全部访问过
        */
        int vertexState[numCourses] = {0};
        

        for(int i = 0; i < numCourses; ++i)
            if(!dfs(i, myVec, vertexState))
                return false;

        return true;
    }

    bool dfs(int node, vector<set<int> >& myVec, int *vertexState) {
        if(vertexState[node] == 1)	return true;
        vertexState[node] = -1;
        for(int i : myVec[node]) {
            if(vertexState[i] == -1)	return false;
            if(!dfs(i, myVec, vertexState))	return false;
        }
        vertexState[node] = 1;
        return true;
    }
};